
 .
.Предложенный метод описания условий сохранения устойчивости макрозообентоценоза к воздействию комбинации факторов позволяет последовательно перейти к решению следующей задачи – количественной оценке и нормированию таких воздействий. Необходимость разработки универсальной меры многофакторной нагрузки на биосистемы вообще и на макрозообентоценозы в частности была обоснована ранее в разделе 1.1. Обобщим обоснованные и выделенные ранее (разд. 1.1, 1.4) критерии, которым должен соответствовать искомый количественный показатель сложного воздействия.
1) Изоболичность. Изоболичность показателя воздействия по отношению к какой-либо k-й из m учитываемых функций благополучия (k={1,…, m}) заключается в том, что каждое его значение должно полностью соответствовать её определённой изоболе (т.е. всем тем и только тем сочетаниям значений комбинируемых факторов, которые вызывают некое одинаковое изменение значения k-й функции). Только при соблюдении этого условия показатель детерминирует реакцию соответствующей характеристики макрозообентоценоза на данное воздействие и, следовательно, может служить аргументом k-й функции благополучия.
Если изоболы m учитываемых функций благополучия макрозообентоценоза подобны, следовательно, данный показатель может служить аргументом всех этих функций, т.е. полностью определяет изученную реакцию сообщества на данное воздействие.
2) Адекватный учёт взаимодействия факторов. Реальный эффект взаимодействия факторов, уникальный в каждой их конкретной комбинации, определяет специфическую форму изобол и, соответственно, значительно влияет на уровень результирующего многофакторного воздействия. Поэтому он должен иметь адекватное количественное выражение, а не сводиться a priori к аддитивности, мультипликативности или какой-либо иной примитивной единообразной форме.
3) Нормировка относительно предельно допустимого уровня (ПДУ). Поскольку комбинируемые факторы имеют разную размерность, искомый изоболический показатель должен быть безразмерным: выражать кратность превышения результирующим многофакторным воздействием его же предельно допустимый уровень.
5.1. Количественная оценка многофакторных антропогенных воздействий на макрозообентоценозы
Предельно допустимый уровень многофакторного воздействия на макрозообентоценоз определяется в гиперпространстве факторов (x1,..., xi,..., xn) границей ОСУ, т.е. n-мерной изоболой повышенного риска потери данным сообществом упругости (разд. 3.4.2).
Конкретная j-я комбинация эмпирических или произвольных значений n взаимодействующих факторов в системе координат (x1,..., xi,..., xn) может быть определена точкой Aj, сопоставленной соответствующим факторным значениям (x1Aj;...; xiAj;...; xnAj).
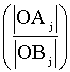
Точка Aj, не принадлежащая ОСУ, очевидно, принадлежит иной n-мерной изоболе. При подобии этой изоболы ОСУ их соотношение может быть количественно выражено отношением евклидовых расстояний от начала координат O (x1=0,…, xi=0,…, xn=0) до точки Aj и от O до точки пересечения отрезком [ OAj] границы ОСУ (точка Bj c координатами (x1Bj;...; xiBj;...; xnBj)):

 .
.
Таким образом, кратность превышения многофакторным воздействием своего предельно допустимого уровня (Y), соответствующая j-й комбинации эмпирических или произвольных значений n учитываемых факторов (Yj), может быть выражена соотношением евклидовых расстояний в гиперпространстве (x1,..., xi,..., xn) от начала координат до точек Aj и Bj:
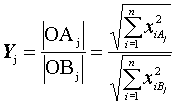 .
. (37)
(37)
Однако, практическое применение формулы (37) для расчёта уровня воздействия Yj затруднено, поскольку для конкретной комбинации эмпирических факторных значений Aj (x1A;...; xiA;...; xnA) нельзя непосредственно определить координаты соответствующей точки Bj, необходимые для расчёта расстояния 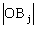 . Более удобно оценивать уровень воздействия Yj опосредованно, взяв за основу формулу границы ОСУ (34). Рассмотрим такую процедуру количественной оценки воздействия в порядке возрастания количества комбинируемых факторов, подобно тому, как это было сделано в предыдущей главе при пояснении способа описания границы ОСУ.
. Более удобно оценивать уровень воздействия Yj опосредованно, взяв за основу формулу границы ОСУ (34). Рассмотрим такую процедуру количественной оценки воздействия в порядке возрастания количества комбинируемых факторов, подобно тому, как это было сделано в предыдущей главе при пояснении способа описания границы ОСУ.
5.1.1. Оценка однофакторного воздействия
При однофакторном воздействии на макрозообентоценоз граница ОСУ соответствует границе диапазона толерантных значений фактора. Кратность превышения воздействием предельно допустимого уровня (Y) соответствует значению данного фактора, нормированному относительно субоптимального диапазона согласно уравнениям (17) (Y = x):
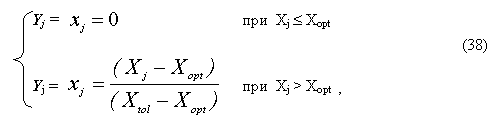
где Xj и xj – абсолютное и нормированное j-е значение фактора X, соответственно.
Например:
– вариации подпороговых, не лимитирующих макрозообентоценоз (оптимальных) значений фактора не учитываются, поэтому в их оптимальном диапазоне значение Y = 0;
– при Y = 0.5 воздействие достигло лишь 50% своего предельно допустимого уровня, упругость сообщества сохраняется;
– при Y = 1.0 воздействие достигло своего предельно допустимого уровня, возникла ситуация повышенного риска потери упругости сообщества;
– при Y = 2.3 – воздействие превысило предельно допустимый уровень в 2.3 раза, сообщество утратило упругость и претерпевает дальнейшую деградацию и т.д.
Если значение Y меньше единицы, упругость сообщества сохраняется, а величина (1–Y) показывает "запас прочности" макрозообентоценоза к данному виду воздействия – предельно допустимую дополнительную нагрузку, не приводящую к потере упругости. В частности, при однофакторном лимитировании величина (1–Y) = (1–x) показывает "запас прочности" к воздействию конкретного лимитирующего фактора.
Согласно (17), сообщество, испытывающее воздействие единственного лимитирующего фактора X, при j-м значении последнего (Xj) может выдержать, сохраняя устойчивость, дополнительное приращение абсолютных значений данного фактора, меньшее или равное Xjдоп:
Xjдоп = Xtol – Xj = ( 1 – xj) (Xtol– Xopt).
 (39)
(39)
Например:
– при Yj = xj = 0.7 такой "запас прочности" макрозообентоценоза составляет 0.3, или 30% от максимального, имевшегося у сообщества по отношению к данному фактору в фоновых условиях; следовательно, макрозообентоценоз может выдержать, сохраняя устойчивость, дополнительное воздействие фактора X (Xjдоп), меньшее или равное 0.3 величины субоптимального диапазона (Xtol– Xopt);
– при Yj = xj = 1.0 "запас прочности" исчерпан (Xjдоп=0), возникает ситуация повышенного риска потери упругости.
Пример 7
. Здесь удобно снова использовать ситуацию однофакторного (теплового) воздействия на макрозообентос песчаной литорали р. Прони, описанную ранее в примерах № 1 (разд. 3.2) и № 4 (разд. 4.3.1). Как было показано, по мере приближения к сбросным каналам ГРЭС в водоёме-охладителе происходит закономерное увеличение уровня термофикации вод. Этот уровень корректно оценивается нормированным показателем l (0 < l < 1), равным соотношению величины подогрева вод в данной точке акватории и синхронной величины максимального подогрева вод в водосбросном канале электростанции (16). Обе эти характеристики существенно варьируют во времени, однако их соотношение, выражаемое показателем l , всегда остаётся практически постоянным и поэтому достаточно точно характеризует степень локального теплового воздействия на экосистему (разд. 4.3.1).Напомним, что потеря упругой устойчивости макрозообентоценоза к тепловому воздействию происходит при
l » 0.2 и носит резкий, скачкообразный характер. Она проявляется в потере целой группы видов, характерных для сообщества в фоновых условиях (из 34 характерных видов исчезает 16, т.е. 47 %), сопровождается значительным уменьшением значений количественных структурно-функциональных ценотических характеристик и интерпретируется как "первая катастрофа" макрозообентоценоза.Дальнейшее поступление теплоты, происходящее по мере приближения к сбросным каналам электростанции, не вызывает значимых изменений макрозообентоса, пока значение показателя термофикации
l не достигает 0.5. Это значение соответствует среднегодовому превышению температуры воды над ее синхронными фоновыми значениями на 4.5 – 5.0 оC. При данном уровне термофикации повторно происходит резкое обеднение видового состава макрозообентоценоза, которое может быть интерпретировано как "вторая катастрофа" (табл. 11). Действительно, из 18 характерных видов, уцелевших после первой катастрофы, совместно исчезают сразу 13: малощетинковые черви Limnodrilus udekemianus и Lumbriculus variegatus, брюхоногие моллюски Valvata depressa, V. ambigua, Physa fontinalis и Lymnaea stagnalis, личинки хирономид Cricotopus gr. sivestris, Polypedilum gr. nubeculosum, P. gr. convictum, P. scalaenum, Microchironomus tener, Procladius ferrugineus и P. choreus. Таким образом, в сообществе остается лишь 5 наиболее эврибионтных характерных видов (т.е. 15% от их исходного количества): малощетинковые черви Tubifex tubifex и Limnodrilus hoffmeisteri, моллюски Dreissena polymorpha и Bithynia tentaculata, личинки хирономид Chironomus f.l. plumosus. Эврибионтный вид Tubifex tubifex в условиях сильного подогрева (l >0.5) существенно увеличивает свою плотность, становясь по этому показателю доминантом деградировавшего донного сообщества.Таблица 11.
Изменение состава видов, характерных для макрозообентоценоза песчаной рипали р. Прони, после первой и второй катастроф, вызванных термофикацией
|
№ |
Виды, характерные в фоновых условиях ( |
% |
Наличие особей |
Наличие особей |
|
1 |
Dreissena polymorpha |
> 99 |
ґ |
ґ |
|
2 |
Bithynia tentaculata |
> 99 |
ґ |
ґ |
|
3 |
Anisus acronicus |
> 99 |
0 |
0 |
|
4 |
Glyptotendipes gripekoveni |
> 99 |
0 |
0 |
|
5 |
Demicryptochironomus gr. vulneratus |
> 99 |
0 |
0 |
|
6 |
Unio longirostris |
> 99 |
0 |
0 |
|
7 |
Pseudoanodonta sp. |
> 99 |
0 |
0 |
|
8 |
Polypedilum gr. nubeculosum |
> 99 |
ґ |
0 |
|
9 |
Valvata depressa |
> 99 |
ґ |
0 |
|
10 |
Lumbriculus variegatus |
> 99 |
ґ |
0 |
|
11 |
Cricotopus gr. sivestris |
> 99 |
ґ |
0 |
|
12 |
Physa fontinalis |
> 99 |
ґ |
0 |
|
13 |
Lymnaea stagnalis |
> 99 |
ґ |
0 |
|
14 |
Limnodrilus hoffmeisteri |
> 99 |
ґ |
ґ |
|
15 |
Tubifex tubifex |
> 99 |
ґ |
ґ |
|
16 |
Bezzia nobilis |
96 |
0 |
0 |
|
17 |
Palpomyia lineata |
96 |
0 |
0 |
|
18 |
Anodonta minima |
96 |
0 |
0 |
|
19 |
Dicrotendipes tritomus |
96 |
0 |
0 |
|
20 |
Procladius ferrugineus |
96 |
ґ |
0 |
|
21 |
Procladius choreus |
96 |
ґ |
0 |
|
22 |
Lipiniella arenicola |
95 |
0 |
0 |
|
23 |
Valvata ambigua |
95 |
ґ |
0 |
|
24 |
Polypedilum scalaenum |
94 |
ґ |
0 |
|
25 |
Tanytarsus pallidicornis |
94 |
0 |
0 |
|
26 |
Limnodrilus udekemianus |
93 |
ґ |
0 |
|
27 |
Mystacides niger |
93 |
0 |
0 |
|
28 |
Microchironomus tener |
93 |
ґ |
0 |
|
29 |
Unio tumidus |
92 |
0 |
0 |
|
30 |
Cyrnus flavidus |
92 |
0 |
0 |
|
31 |
Polypedilum gr. convictum |
92 |
ґ |
0 |
|
32 |
Somatochlora metallica |
91 |
0 |
0 |
|
33 |
Stylaria lacustris |
91 |
0 |
0 |
|
34 |
Chironomus f.l. plumosus |
90 |
ґ |
ґ |
|
Примечание: 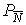 – достоверность отличия от нуля средней арифметической популяционной плотности за период наблюдений; "ґ " и "0" – присутствие и отсутствие особей указанного вида в данных условиях, соответственно; виды ранжированы по убыванию значений – достоверность отличия от нуля средней арифметической популяционной плотности за период наблюдений; "ґ " и "0" – присутствие и отсутствие особей указанного вида в данных условиях, соответственно; виды ранжированы по убыванию значений 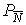 . . |
||||
Общее количество всех видов макрозообентоса, особи которых обнаружены в биотопе хотя бы однократно, при
l >0.5 составляет всего 11 против 76 в фоновых условиях, т.е. тоже не более 15 %. Однако отсутствие в пробах особей нехарактерных видов, как пояснялось выше, менее доказательно и не может считаться надёжным биоиндикационным признаком.Описанное повторное обеднение видового состава бентоса песчаной рипали при
l » 0.5, или вторая катастрофа, приводит к окончательной деградации сообщества (рис. 29). Значения количественных характеристик макрозообентоса изменяются при этом также скачкообразно и после второй катастрофы не превышают 10-20 % от своих фоновых значений. Уцелевшие виды зообентоса эврибионтны настолько, что способны стабильно существовать даже при максимальном подогреве (при l ® 1), т.е. непосредственно в сбросных каналах, куда поступают сточные термальные воды ГРЭС.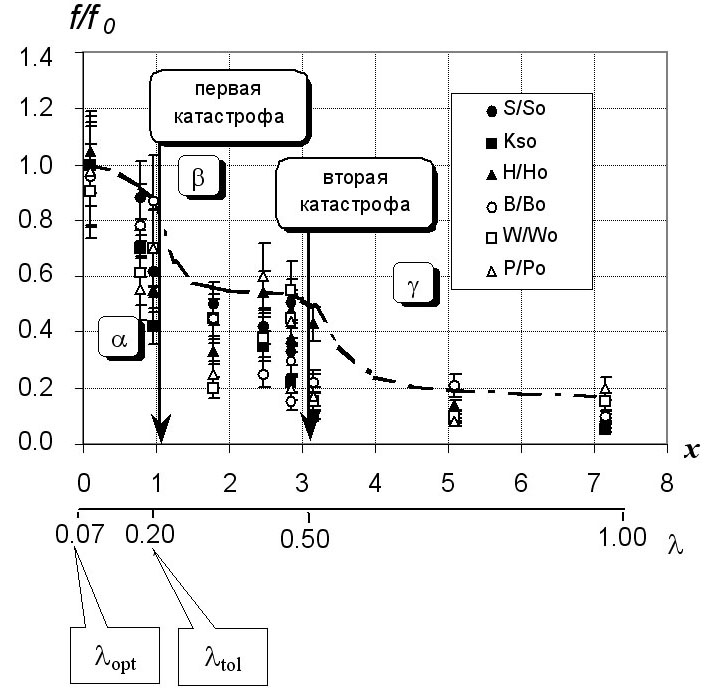
Рис. 29. Графики функций благополучия макрозообентоценоза песчаной рипали водоёма-охладителя Рязанской ГРЭС в условиях теплового воздействия, выражаемого показателями
l и x.
5.1.2. Оценка двухфакторного воздействия
При воздействии на макрозообентоценоз двух факторов X1 и X2 (или, после нормировки их значений по уравнениям (18) и (19), x1 и x2) граница ОСУ описывается формулой (20). Форма графика уравнения (20) (как и форма тех изобол любой другой функции благополучия, которые подобны ОСУ) определяется значениями параметров Z1 и Z2, количественно выражающих характер взаимодействия факторов.
Допустим, требуется оценить уровень результирующего воздействия (Y) на макрозообентоценоз, создаваемого факторами x1 и x2, при каком-либо произвольном или эмпирическом j-м сочетании их значений (x1j и x2j), не принадлежащем границе ОСУ. Граница ОСУ описана уравнением (20), установлены значения его параметров Z1 и Z2 (разд. 4.3.2). Очевидно, что сочетание значений факторов x1j и x2j в системе координат (x1, x2) принадлежит некой изоболе, отличной от ОСУ. Если эта изобола подобна ОСУ, она может быть описана формулой, гомологичной формуле (20):
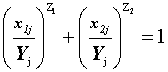 ,
, (40)
(40)
где Yj – кратность превышения предельно допустимого уровня воздействием, создаваемым j-й комбинацией значений факторов x1 и x2 (x1j, x2j).
Согласно (37), значение показателя двухфакторного воздействия Y, соответствующее j-й комбинации эмпирических факторных значений (Yj), может быть выражено соотношением евклидовых расстояний в гиперпространстве (x1, x2) от точки начала координат до точек Aj и Bj (рис. 30):
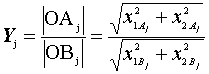 ,
,  (41)
(41)
где точка Aj с координатами (x1Aj; x2Aj) – j-е сочетание эмпирических значений факторов x1 и x2; Bj с координатами (x1Bj; x2Bj) – точка пересечения отрезком [ОАj] границы ОСУ.
Если изобола, которой принадлежит точка Aj, подобна границе ОСУ, то соотношение расстояний от начала координат до любой точки Aj , принадлежащей данной изоболе (A1, A2,…, Aj,…), и от начала координат до соответствующей точки пересечения отрезка [OAj] с границей ОСУ (B1, B2,…, Bj,…) является величиной постоянной, равной Yj:
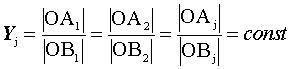 .
.  (42)
(42)
Оценим соответствие показателя двухфакторного воздействия Y трём критериям, выделенным в начале этой главы.
1) Изоболичность. Если изоболы некой функции благополучия подобны ОСУ, то каждое конкретное значение показателя Y объединяет те и только те сочетания значений факторов x1 и x2, которые определяют единственное соответствующее им значение данной функции. Таким образом, показатель двухфакторного воздействия Y детерминирует изоболы, подобные ОСУ, и является для таких функций благополучия изоболическим.
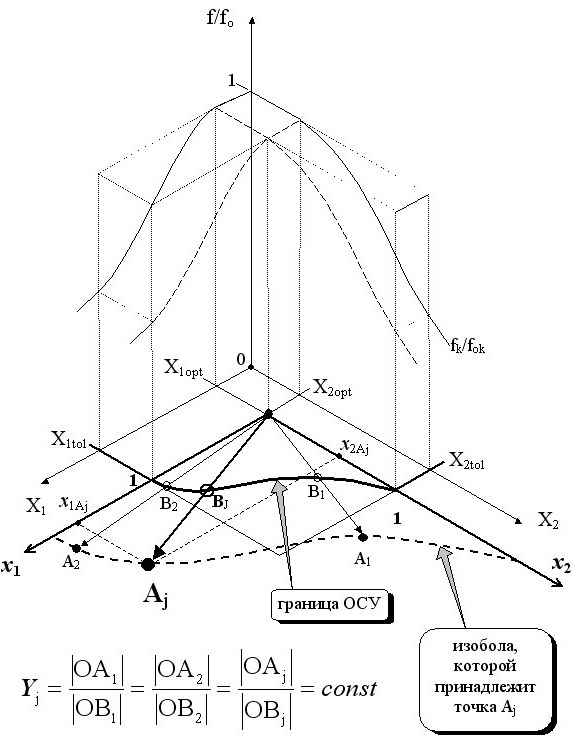
Рис. 30. Оценка кратности превышения устойчивости макрозообентоценоза (Y) к воздействию двух факторов (X1, X2) для конкретного сочетания их значений (точка Aj с координатами (x1Aj; x2Aj)). Bj – точка пересечения отрезком [OAj] границы ОСУ. Остальные обозначения в тексте.
2) Адекватный учёт взаимодействия факторов обеспечивается использованием эмпирических значений параметров Z1 и Z2 уравнения (40), описывающего как границу ОСУ (если Y = 1), так и любые подобные ей изоболы других функций благополучия.
Подчеркнём, что подобие различных изобол любой анализируемой функции благополучия границе ОСУ и друг другу является необходимым условием изоболичности показателя Y для данной функции и, как следствие, возможности корректного использования в качестве её аргумента (рис. 31).
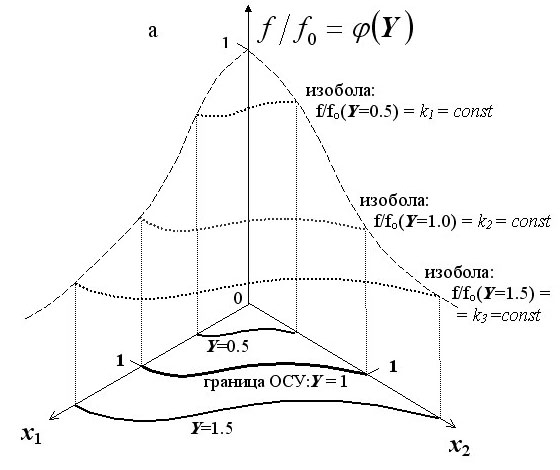
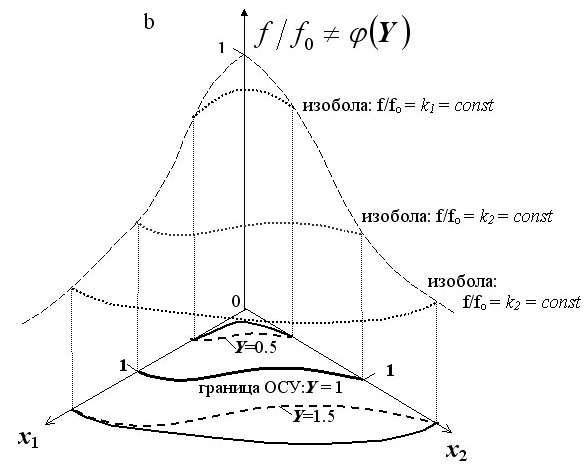
Рис. 31. Подобие изобол – необходимое условие использования показателя Y как аргумента функций благополучия макрозообентоценозов от многофакторного воздействия (f/f0 = j
(Y)).
a: Изоболы подобны другу и, в частности, границе ОСУ; конкретному значению Y соответствует одно значение функции благополучия, изоболы функции благополучия описываются формулой (40); показатель Y является изоболическим; f/f0 = j
(Y).
b: Изоболы не подобны другу и, в частности, границе ОСУ; конкретному значению Y соответствуют различные значения функции благополучия, изоболы функции благополучия не описываются формулой (40); показатель Y не является изоболическим; f/f0 ≠ j
(Y).
Действительно, если различные изоболы некой функции благополучия макрозообентоценоза подобны границе ОСУ, то, согласно формуле (40), каждому значению Y будет соответствовать только одно значение данной функции (рис. 31a). Следовательно, показатель многофакторного воздействия Y может служить аргументом такой функции благополучия.
Если же изоболы функции благополучия не подобны друг другу и (или) не подобны границе ОСУ, то каждому значению Y будет соответствовать множество значений данной функции (рис. 31b). Показатель Y не является для такой функции изоболическим и, следовательно, не должен использоваться как её аргумент.
Таким образом, если изоболы различных функций благополучия макрозообентоценоза не подобны, то принципиально невозможно разработать такой показатель многофакторного воздействия, который являлся бы изоболическим для всех этих функций. Поэтому наиболее важным следует считать обеспечение изоболичности показателя многофакторного воздействия относительно той функции благополучия, которая характеризует основное свойство макрозообентоценоза и имеет наибольшую биоиндикационную ценность. Такой основной функцией благополучия макрозообентоценоза является его упругая устойчивость к воздействию (разд. 3.4), имеющая единственную изоболу – границу ОСУ. Поэтому наиболее целесообразно оценивать уровень двухфакторного воздействия, сравнивая его именно с границей ОСУ, согласно формуле (40). Если же биоиндикация осуществляется также с использованием нескольких других, вспомогательных функций благополучия макрозообентоценоза, целесообразно проверить, может ли показатель воздействия Y считаться изоболическим для каждой из них.
3) Нормировка относительно ПДУ. Безразмерный показатель Y выражает кратность превышения результирующим двухфакторным воздействием своего предельно допустимого уровня. В зависимости от силы результирующего воздействия двух факторов на макрозообентоценоз, значения Y теоретически могут варьировать от 0 до +Ґ . Примеры интерпретации различных значений показателя приведены выше, в разделе 5.1.1. При Y < 1 "запас прочности" макрозообентоценоза к воздействию оценивается как 1–Y (см. разд. 5.1.1).
Таким образом, предлагаемый показатель двухфакторного воздействия (Y) демонстрирует максимальное возможное соответствие всем трём вышеуказанным критериям.
Значение Y не может быть вычислено непосредственно по формуле (40). Расчёт кратности превышения предельно допустимого уровня воздействием, создаваемым j-м сочетанием значений двух факторов (Yj), согласно формуле (40), осуществляется путём поиска минимума функции:
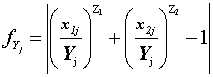 .
.  (43)
(43)
Для этого требуется заранее определить значения параметров Z1 и Z2, описав границу ОСУ формулой (20) (разд. 4.3.2). Для любого произвольного или эмпирического j-го сочетания значений факторов x1 и x2 (x1j, x2j) существует лишь одно искомое значение показателя Y (Yj), при котором значение функции (43) становится равным нулю, а формула (40) становится верным равенством.
Расчет значений Yj при изучении двухфакторного лимитирования макрозообентоценозов производился нами с использованием пакета программ MS-Excel. Поиск минимума функции (43) осуществлялся методами Ньютона и Градиентного спуска, дававшими одинаковую оценку уровня двухфакторного воздействия Y. Показатель определялся с точностью до второй значащей цифры, что позволяло избежать избыточной точности получаемых результатов. При этом расчётные значения Y переставали меняться в пятом знаке не позднее, чем после 10-й итерации, во втором знаке – после 3-й – 5-й итерации.
Пример 8
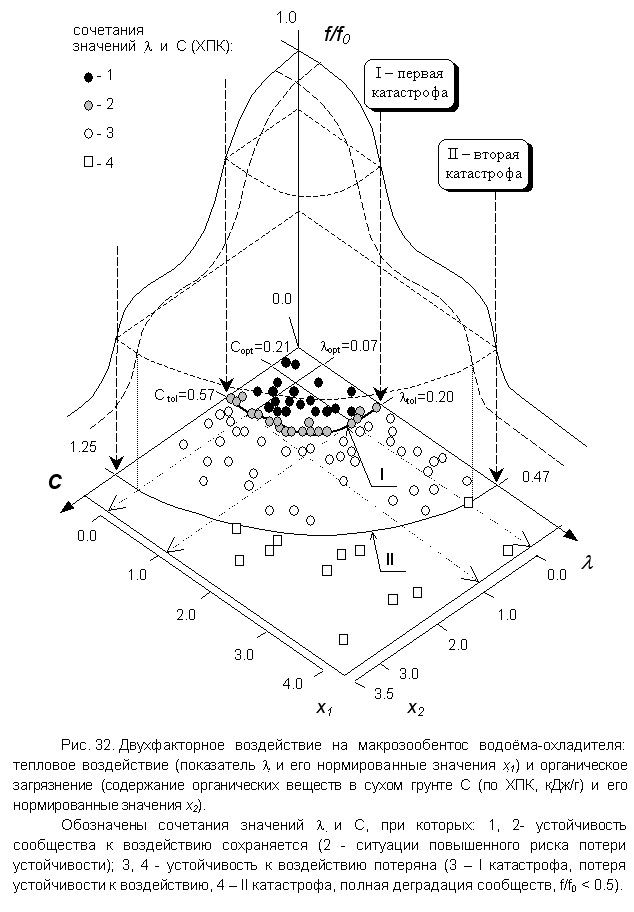
. Двухфакторное воздействие на макрозообентос модельного биотопа заиленной медиали водоёма-охладителя Рязанской ГРЭС, создаваемое сочетанием термофикации и органического загрязнения от садковых линий, подробно охарактеризовано в примере № 5 к разделу 4.3.2. Там же продемонстрирована процедура описания ОСУ макрозообентоценоза к данному воздействию и формализованы условия сохранения упругой устойчивости донного сообщества. Воспользуемся этим же объектом для иллюстрации количественной оценки двухфакторного воздействия на макрозообентос с использованием изоболического показателя Y.Реакция видового состава макрозообентоценоза на данное воздействие и типичный график функции благополучия сообщества от двух указанных факторов отражены на рисунке 32. На рисунке 33 представлен конкретный график одной из функций благополучия макрозообентоценоза (видовое богатство, или количество зарегистрированных видов в сообществе, нормированное относительно своего фонового значения) от данных факторов (рис. 33a) и от изоболического показателя их совместного действия Y (рис. 33b).
Как было показано в примере № 5, ситуации повышенного риска потери упругой устойчивости макрозообентоценоза к двухфакторному воздействию легко опознавались при ведении натурных исследований, поскольку эта потеря имела явно катастрофический характер. Сообщество утрачивает сразу около половины характерных видов, а значения функций его благополучия снижаются в среднем на 60 % (40 ё 80 %). Граница ОСУ описана уравнением (25), а условия сохранения упругой устойчивости макрозообентоценоза к данному двухфакторному воздействию – неравенством (26).
Следовательно, показатель результирующего двухфакторного воздействия на макрозообентос Y, в соответствии с формулами (25) и (40), должен рассчитываться по формуле:
. 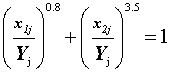 .
. (44)
(44)
Изоболы большинства функций благополучия макрозообентоценоза могут с приемлемой точностью считаться подобными границе ОСУ (рис. 32, 33).
По мере дальнейшей интенсификации воздействия до некоторых пределов макрозообентоценоз не испытывает существенных изменений. Однако при определённых сочетаниях значений уровня термофикации и органического загрязнения вторично происходит резкое структурное изменение сообщества, описанное в предыдущем примере (применительно к бентосу песчаной рипали) как вторая катастрофа. В илистой медиали вторая катастрофа макрозообентоценоза также проявляется довольно отчётливо. Из сообщества исчезает ещё около 40 % видов, характерных для него в фоновых условиях. После этого в его составе остаётся не более 5 характерных видов, наиболее эврибионтных.
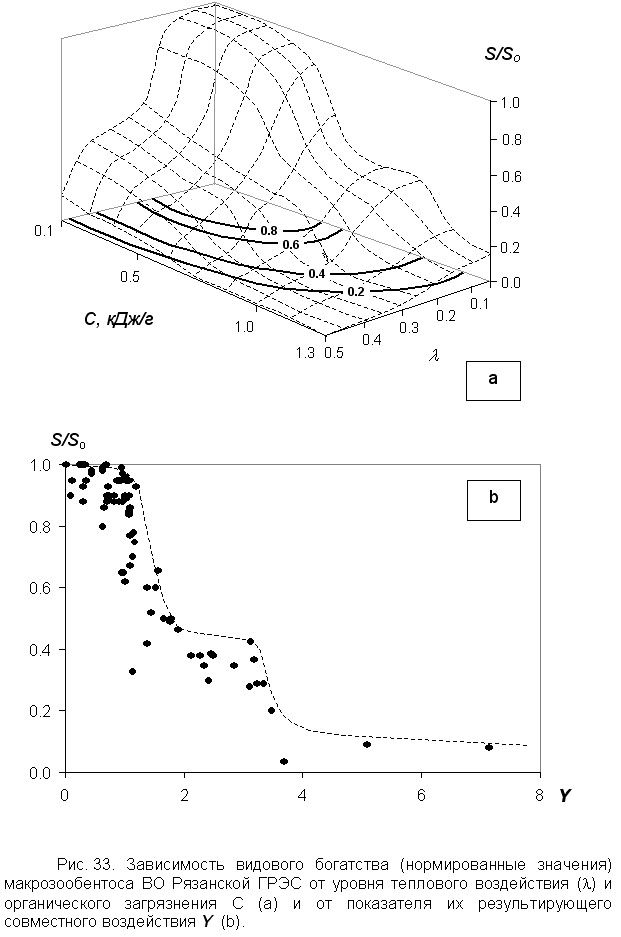
На большинстве станций, характеризующих бенталь после второй катастрофы, макрозообентос представлен лишь двумя-тремя видами, а некоторые участки дна здесь вообще лишены какой-либо макрофауны. Значения функций благополучия макрозообентоценоза, за исключением характеристик обилия тотального бентоса, обычно составляют после второй катастрофы около 15 % (0
ё 30 %) от своих фоновых значений. Таким образом, в заиленной медиали, как и в рипали, вторая катастрофа практически приводит макрозообентоценоз к полной деградации.Изобола, соответствующая второй катастрофе макрозообентоценоза, может с удовлетворительной точностью считаться подобной границе ОСУ в системе координат, сопоставленных нормированным значениям двух указанных факторов. Это позволяет описать условия второй катастрофы макрозообентоценоза, подставив в формулу (44) соответствующее конкретное значение изоболического показателя Y =3.3 (рис. 32, 33):
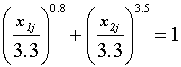 .
. (45)
(45)
Иными словами, уровень данного двухфакторного воздействия, вызывающий вторую катастрофу сообщества, в 3.3 раза превышает уровень, вызывающий потерю его упругой устойчивости и связанную с этим первую катастрофу. Соответственно, условия двухфакторного воздействия, позволяющие избежать второй катастрофы, могут быть описаны неравенством:
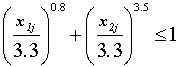 .
. (46)
(46)
Очевидно, что описание границы ОСУ требует гораздо меньшего количества эмпирического материала, чем описание условий второй катастрофы сообщества (рис. 32). Изобола, соответствующая второй катастрофе, описывается в двухфакторной системе координат намного более длинным отрезком кривой, чем граница ОСУ. Кроме того, пограничные ситуации, соответствующие второй катастрофе, по сравнению с ситуациями повышенного риска потери упругой устойчивости, рассеяны в бентали охладителя гораздо менее упорядоченно, что затрудняет их поиск и обнаружение в достаточном количестве. В связи с этим изобола, соответствующая второй катастрофе, возможно, описана с меньшей точностью, чем граница ОСУ. Вероятно, дополнительный целевой сбор недостающих материалов позволил бы несколько уточнить значение изоболического показателя, соответствующее второй катастрофе.
5.1.3. Оценка многофакторного воздействия
Граница ОСУ макрозообентоценоза, испытывающего комбинированное воздействие n факторов X1,…, Xi,…, Xn (или, после нормировки их значений по уравнениям (27), x1,…, xi,…, xn), описывается формулой (34). При этом форма n-мерной поверхности, описывающей границу ОСУ, определяется значениями параметров Z1,…, Zi,…, Z n, отражающих характер взаимодействия каждого i-го фактора с остальными n–1 факторами (разд. 4.3.3).
Оценка кратности превышения n-факторным воздействием своего предельно допустимого уровня (Y) может быть осуществлена в общем так же, как и при двухфакторном воздействии.
Допустим, следует оценить уровень результирующего воздействия (Y) на макрозообентоценоз, создаваемое произвольным или эмпирическим j-м сочетанием значений n комбинированных факторов (x1j,…, xij,…, xnj), которое не принадлежит границе ОСУ. Гипотетический пример такой ситуации для трёхфакторного воздействия (n=3) приведён на рисунке 34. Сопоставим данное сочетание факторных значений точке Aj в системе координат (x1,…, xi,…, xn). Точка Aj с координатами (x1j;…; xij;…; xnj) принадлежит некой изоболе. Если данная изобола подобна ОСУ, то она может быть описана формулой, гомологичной формулам (34) и (40):
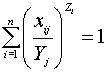 ,
, (47)
(47)
где Yj – кратность превышения предельно допустимого уровня воздействием, создаваемым j-й комбинацией значений факторов x1,…, xi,…, xn.
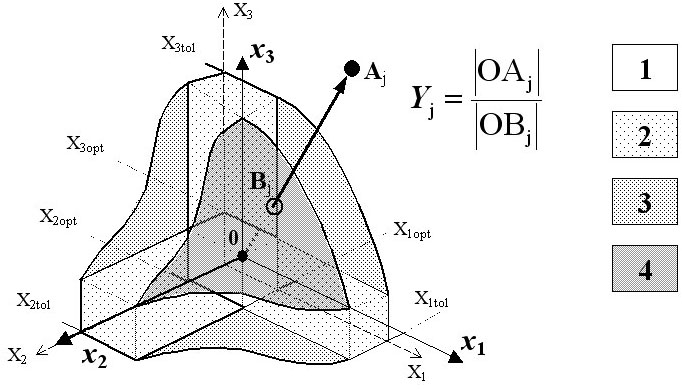
Рис. 34. Оценка кратности превышения устойчивости макрозообентоценоза (Y) к воздействию трёх факторов (X1, X2, X3) для конкретного j-го сочетания их значений (точка Aj). Точка Bj – пересечение отрезком [OAj] границы ОСУ. Остальные обозначения в тексте.
Область сохранения устойчивости в воздействию:
1) значения всех трех факторов оптимальны;
2) значения двух факторов оптимальны, одного – субоптимальны;
3) значения одного фактора оптимальны, двух – субоптимальны;
4) значения всех трех факторов субоптимальны.
Формула (47) соответствует уравнению (37), но при этом даёт более удобный подход к определению кратности превышения воздействием своего предельно допустимого уровня (Y). Значение Yj не может быть вычислено непосредственно по формуле (47), но может быть легко рассчитано путём поиска минимума функции:
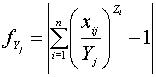 .
. (48)
(48)
Для этого требуется заранее установить значения параметров Z1,…, Zi,…, Zn, дающие наиболее точное описание границы ОСУ, согласно формулам (34), (35) (разд. 4.3.3). Для любого произвольного или эмпирического j-го сочетания значений факторов (x1j,…, xij,…, xnj) существует лишь одно искомое значение показателя Y (Yj), при котором значение функции (48) становится равным нулю, а формула (47) превращается в верное равенство.
Расчет значений Yj при изучении многофакторного лимитирования макрозообентоценозов производился нами с использованием пакета программ MS-Excel. Поиск минимума функции (48) осуществлялся методами Ньютона и градиентного спуска, неизменно дававшими одинаковую оценку величины Y. Показатель определялся с точностью до второй значащей цифры. Расчётные значения Y переставали меняться во втором знаке не позднее, чем после 3-й – 7-й итерации.
В заключение настоящего раздела следует оценить соответствие предлагаемой количественной меры многофакторного воздействия на макрозообентоценоз трём сформулированным ранее критериям.
1) Изоболичность. Показатель многофакторного воздействия Y является изоболическим для всех функций благополучия, изоболы которых подобны ОСУ. Каждое конкретное значение Y детерминирует определённую изоболу, подобную ОСУ: включает те и только те сочетания значений факторов x1,…, xi,…, xn, которые определяют единое значение соответствующей характеристики макрозообентоценоза.
Адекватность и правомочность использования показателя результирующего многофакторного воздействия Y как аргумента конкретной функции благополучия макрозообентоценоза зависит от того, подобны ли изоболы данной функции друг другу и ОСУ (см. разд. 5.1.2).
2) Адекватный количественный учёт эффекта взаимодействия факторов обусловливается использованием эмпирических значений параметров Z1,…, Zi,…, Zn уравнения (47), описывающего как границу ОСУ (если Y = 1), так и любые подобные ей изоболы других функций благополучия макрозообентоценоза.
3) Нормировка относительно ПДУ. Показатель Y выражает кратность превышения результирующим двухфакторным воздействием своего предельно допустимого уровня. В зависимости от силы результирующего многофакторного воздействия на макрозообентоценоз, значения Y теоретически могут варьировать от 0 до 1 при сохранении упругости и от 1 до +Ґ при её утрате. Примеры интерпретации различных значений показателя приведены выше, в разделе 5.1.1.
Таким образом, предлагаемый показатель (Y) характеризуется максимальным возможным соответствием всем трём выделенным критериям и может использоваться как адекватная мера комбинированного внешнего воздействия на макрозообентоценоз при любом количестве взаимодействующих факторов.
Пример 9
. В примере № 6 к разделу 4.3.3. был подробно проиллюстрирован расчёт устойчивости макрозообентоса рек Паши и Капши к пятифакторному антропогенному воздействию. В результате были получены соответствующие параметры уравнения (34), описывающего границу ОСУ макрозообентоценозов к комбинированному действию совокупности внешних факторов. Полученные параметры уравнения приведены в таблице 10.Соответственно, изоболический показатель результирующего пятифакторного воздействия на макрозообентос Y должен рассчитываться по формуле (47) при n=5 с параметрами, указанными в таблице 10:
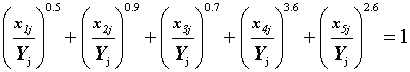 .
.  (49)
(49)
Поскольку значение показателя Y может быть корректно сопоставлено изоболе какой-либо функции благополучия лишь в том случае, если эта изобола подобна границе ОСУ, целесообразно проверить, какие именно характеристики макрозообентоса отвечают данному условию. В частности, можно сделать это следующим способом.
Изобола, определяющая конкретное значение какой-либо функции благополучия, может быть описана уравнением, аналогичным (34). Для этого абсолютные значения факторов тоже нормируются относительно границ соответствующих диапазонов оптимальных и толерантных значений, определяемых для данной конкретной изоболы путём сравнительного анализа проекций, аналогично тому, как это описано в разделе 4.3.3. Различие состоит лишь в критерии отбора тех эмпирических сочетаний факторных значений, которые будут учтены в дальнейшем расчёте. При описании границы ОСУ отбирались лишь те сочетания факторных значений, которые создают ситуации повышенного риска потери сообществом упругой устойчивости. Здесь же таким критерием отбора является принадлежность нормированного значения функции благополучия, задаваемого данным сочетанием факторных значений, определённому интервалу D k:
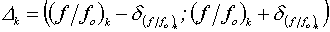 ,
,  (50)
(50)
где 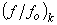 – k-е значение данной функции благополучия,
– k-е значение данной функции благополучия, 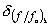 – допустимая погрешность этого значения.
– допустимая погрешность этого значения.
Расчет параметров Z для такого уравнения, аналогичного (34), также осуществляется методом наименьших квадратов, при поиске минимума функции, аналогичной, соответственно, функции (35). В результате выявляется искомое сочетание значений Z1,…, Zn, при котором n-мерная поверхность пройдёт в максимальной возможной близости ко всем тем эмпирическим сочетаниям нормированных факторных значений, которые соответствуют критерию 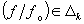 . Дальнейшее сравнение значений показателей степени Z, полученных для данной изоболы, с соответствующими их значениями, описывающими границу ОСУ в уравнении (34), позволяет судить, может ли данная изобола считаться подобной границе ОСУ. Если значения Z, полученные для каждого из факторов двумя указанными способами, оказываются сходными, можно принять изоболу подобной границе ОСУ и, следовательно, описывать её соответствующим конкретным значением изоболического показателя Y, рассчитываемого по формуле (47).
. Дальнейшее сравнение значений показателей степени Z, полученных для данной изоболы, с соответствующими их значениями, описывающими границу ОСУ в уравнении (34), позволяет судить, может ли данная изобола считаться подобной границе ОСУ. Если значения Z, полученные для каждого из факторов двумя указанными способами, оказываются сходными, можно принять изоболу подобной границе ОСУ и, следовательно, описывать её соответствующим конкретным значением изоболического показателя Y, рассчитываемого по формуле (47).
Результаты проверки подобия изобол функции благополучия границе ОСУ иллюстрируются на примере индекса видового разнообразия сообществ (по Шеннону-Уиверу), значения которого нормированы относительно фоновых (табл. 12).
Таблица 12.
Выборочные результаты расчетов значений параметров Zi по результатам описания границы ОСУ (I) и изобол, соответствующих различным постоянным нормированным значениям одной из функций благополучия – видового разнообразия макрозообентоценоза по Шеннону-Уиверу (ZHi) (II)
|
Расчетные значения Zi: |
Факторы: |
|||||
|
Концентрация кислорода в воде |
Органическое загрязнение воды (по ХПК) |
Концентрация фенолов (летучих с паром) |
Концентрация ионов аммония |
Концентрация нефтепродуктов |
||
|
X1 |
X2 |
X3 |
X4 |
X5 |
||
|
Граница ОСУ по уравнению (34) |
I. По описанию ситуаций повышенного риска потери устойчивости (значения Zi) |
|||||
|
0.49 |
0.93 |
0.68 |
3.56 |
2.59 |
||
|
Изоболы H/Ho » const |
II. По различным изоболам значений видового разнообразия, нормированных относительно фоновых (H/Ho) |
|||||
|
|
|
|||||
|
0.80 |
0.75 ё 0.85 |
0.5 |
0.9 |
0.8 |
3.7 |
2.2 |
|
0.65 |
0.60 ё 0.70 |
0.4 |
0.8 |
0.8 |
3.9 |
2.5 |
|
0.50 |
0.45 ё 0.55 |
0.5 |
0.9 |
0.7 |
4.1 |
2.8 |
|
0.35 |
0.30 ё 0.40 |
0.8 |
0.6 |
0.8 |
5.0 |
1.9 |
|
среднее значение ZHi: |
0.6 |
0.8 |
0.8 |
4.2 |
2.4 |
|
Видно, что расчетные значения параметра Z каждого i-го фактора, определённые для различных изобол видового разнообразия (ZHi), в основном довольно сходны, хотя их отдельные значения и могут при этом заметно отклоняться от средних. Средние значения параметров ZHi достаточно близки к соответствующим значениям параметров Zi уравнения (34), описывающего границу ОСУ, различия значений ZH и Z – недостоверны (за исключением единственного параметра Z3, характеризующего синергизм фактора X3 – содержания в воде летучих фенолов). Таким образом, допустимо считать различные изоболы нормированных значений индекса видового разнообразия макрозообентоса подобными друг другу и границе ОСУ и описывать их соответствующими конкретными значениями изоболического показателя Y, определяемого согласно (47).
Аналогично проведена проверка и остальных использованных функций благополучия, перечисленных выше (разд. 4.2; пример № 4 к разд. 4.3.1). Выяснилось, что гипотеза подобия различных изобол друг другу и ОСУ может быть также принята для таких функций благополучия от пяти данных факторов, как видовое богатство (S/Sо), сходство видового состава сообщества с фоновым (KSо), средняя масса особи (W/Wо). Изоболы биомассы макрозообентоса (B/Bо) оказались подобными границе ОСУ и детерминировались изоболическим показателем Y лишь в биотопах с твёрдыми, слабо заиленными грунтами. Для биотопов с мягкими, илистыми субстратами гипотезу подобия различных изобол биомассы макрозообентоса друг другу и границе ОСУ пришлось отвергнуть, так как в этих условиях умеренное воздействие может вызывать несколько более сложный эффект за счёт увеличения популяционных показателей эврибионтных бентонтов (разд. 5.2).
Следует подчеркнуть, что такое описание изобол количественных характеристик бентоса целесообразно осуществлять лишь для проверки гипотезы их подобия друг другу и границе ОСУ. Ни в коем случае не следует заменять таким образом основной метод расчёта устойчивости, изложенный в главе 4, несмотря на его несколько большую трудоёмкость. Определение значений параметров Z по результатам аппроксимации границы ОСУ гораздо более обоснованно, строится на достаточно строгих критериях и даёт намного более точные результаты, чем на основе анализа прочих функций благополучия макрозообентоценоза.
Очевидно, что теоретически показатель результирующего многофакторного воздействия Y должен быть наиболее адекватным аргументом тех функций благополучия, по отношению к которым он является изоболическим. Рассмотрим, как проявляется эта зависимость характеристик макрозообентоса от изоболического показателя Y в экосистеме р. Паши и её притоков. В таблице 13 и на рисунке 35 приводятся некоторые результаты сравнительной оценки зависимости нескольких характеристик бентоса от различных показателей антропогенного воздействия.
В качестве альтернативных зависимых переменных рассматриваются нормированные значения трёх функций благополучия макрозообентоценоза, по отношению к которым показатель Y признан изоболическим (видовое богатство, разнообразие и биомасса макрозообентоса в биотопах с твёрдыми грунтами), а также их абсолютные значения.
В качестве альтернативных независимых переменных используются значения показателя результирующего пятифакторного воздействия Y и значения каждого из этих пяти факторов – как абсолютные (X1,…, X5), так и нормированные по уравнению (27) с параметрами, приведенными ранее в таблице 10 (x1,…, x5).
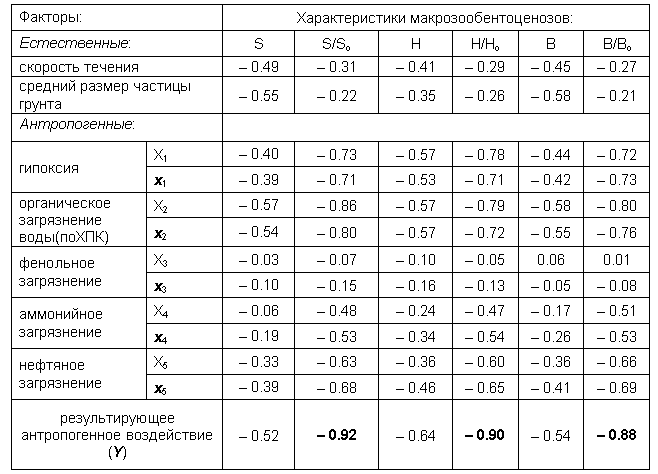
Простейшей мерой зависимости тестируемых биотических характеристик от значений конкретных факторов и от изоболического показателя Y может служить коэффициент корреляции (табл. 13, рис. 35). Зависимость нормированных значений видового разнообразия (H/Ho) от нормированных значений факторов (x1,…, x5) и от показателя Y иллюстрируется также графически (рис. 35).
Представленные результаты показывают, что тенденция лимитирования тестируемых характеристик макрозообентоса каждым из факторов проявляется, в большей или меньшей степени, при всех способах выражения факторных значений, поскольку все значения коэффициента корреляции неизменно отрицательны. Однако сила и достоверность корреляции при этом существенно зависят от выбора сравниваемых переменных.
При сопоставлении абсолютных значений конкретных факторов и ненормированных характеристик сообщества отрицательная корреляция обычно слаба и недостоверна.
Нормировка как значений факторов, так и, особенно, значений функций благополучия, заметно усиливает корреляцию. Это закономерно, поскольку применяемые здесь приемы нормировки этих показателей как раз и предназначены для устранения той доли их общей вариабельности, которая не связана с изучаемым воздействием (разд. 4.2). Так, например, корреляция показателей гипоксии и органического загрязнения со значениями всех трех функций благополучия становится достоверной только при нормировке значений функций благополучия относительно их фоновых значений.
Однако наиболее сильная и достоверная корреляция (r
» 0.9) проявляется между значениями изоболического показателя результирующего пятифакторного воздействия Y и нормированными значениями функций благополучия (выделенные значения коэффициента корреляции в нижней строке табл. 13; рис. 35f).Таблица 13.
Коэффициенты корреляции характеристик макрозообентоценозов и характеристик водной среды (для всех биотопов реки Паши и её притоков, кроме заиленных плёсов)
Примечания:
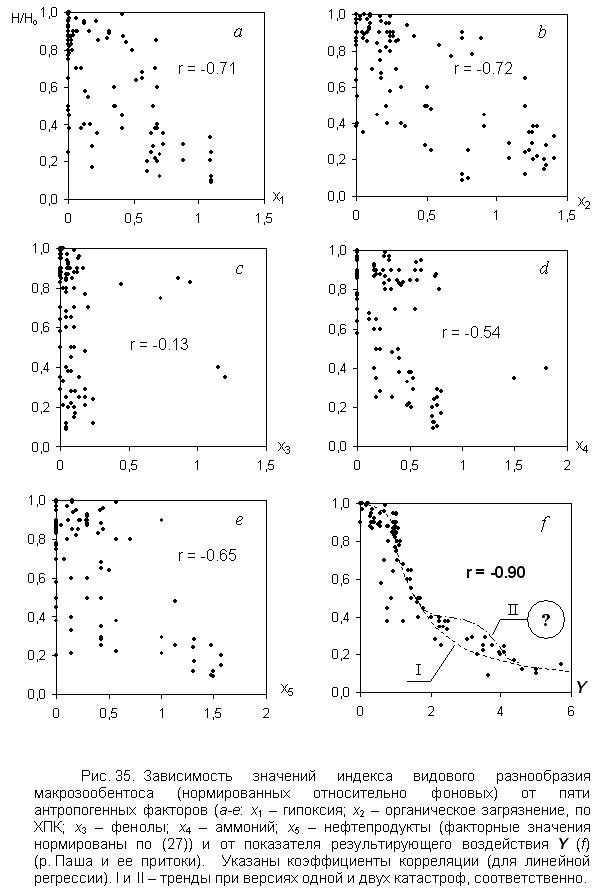
Следует заметить, что, если первая катастрофа сообществ, связанная с потерей упругой устойчивости к воздействию, проявляется при данном пятифакторном воздействии достаточно отчётливо, то вопрос о существовании второй катастрофы здесь остаётся открытым. Несмотря на наличие большого фактического материала, характеризующего пространственную и временную динамику антропогенного воздействия на реку Пашу и её притоки, судить о наличии или отсутствии катастрофической реакции донных сообществ на трёхкратное превышение воздействием упругой устойчивости к нему всё же затруднительно. Довольно показателен в этом отношении пример на рисунке 35f. Несомненно, что при Y>3 сообщества существенно деградируют не только по видовому разнообразию (как это видно на рисунке), но и по всем остальным характеристикам. Однако остаётся неясным, происходит ли эта деградация по мере увеличения воздействия плавно (рис. 35f, I) или же скачкообразно, катастрофически (рис. 35f, II) – наподобие того, как это вполне отчётливо наблюдалось в водоёме-охладителе Рязанской ГРЭС (пример № 8
).Рассмотренный пример достаточно наглядно иллюстрирует соответствие показателя результирующего многофакторного воздействия всем трём выделенным критериям.
Кроме того, к существенным достоинствам данного изоболического показателя относятся также следующие его свойства.
·
Используется необходимое и достаточное количество параметров для каждого из комбинируемых факторов (47): границы диапазонов оптимальных и субоптимальных значений и показатель Z, характеризующий взаимодействие данного фактора с остальными. Все эти параметры имеют самостоятельный смысл, вполне информативны, их значения могут содержательно интерпретироваться и сопоставляться. Таким образом, формула (47) не только служит для расчёта результирующего уровня многофакторного воздействия, но также и характеризует, по выражению А.Ц. Торосяна (1994), основные "механизменные и сущностные стороны описываемого явления".·
Для ситуаций, в которых сообщество уже реагирует на воздействие, но ещё сохраняет упругую устойчивость к нему (0 < Y < 1), имеется возможность количественно оценить "запас прочности" макрозообентоценоза, или его "остаточную устойчивость" –меру предельно допустимого дополнительного воздействия 1–Y, не приводящего к потери упругости.·
Слагаемые формулы (47),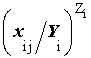 позволяют оценить долевой вклад каждого из комбинируемых факторов в их результирующее воздействие на биоту. При этом для каждого фактора учитывается и кратность превышения соответствующего ПДУ (xij), и эффект его взаимодействия с остальными факторами (Zi). В частности, ранжирование компонентов воздействия в порядке убывания значений показателя
позволяют оценить долевой вклад каждого из комбинируемых факторов в их результирующее воздействие на биоту. При этом для каждого фактора учитывается и кратность превышения соответствующего ПДУ (xij), и эффект его взаимодействия с остальными факторами (Zi). В частности, ранжирование компонентов воздействия в порядке убывания значений показателя 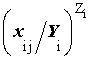 позволяет упорядочить и наглядно сопоставить факторы по величине их реального вклада в совместное лимитирование биоты. Очевидно, что это имеет не только теоретическое, но и важное практическое значение – например, при выборе наиболее эффективных мер по снижению конкретного многофакторного воздействия на гидроэкосистему.
позволяет упорядочить и наглядно сопоставить факторы по величине их реального вклада в совместное лимитирование биоты. Очевидно, что это имеет не только теоретическое, но и важное практическое значение – например, при выборе наиболее эффективных мер по снижению конкретного многофакторного воздействия на гидроэкосистему.
5.2. Закономерности реакции макрозообентоценозов на многофакторное воздействие как основа его нормирования
Использование изоболического показателя Y позволяет выявить и обобщить некоторые основные закономерности реакции макрозообентоса на многофакторные воздействия различного происхождения и разной степени сложности.
По мере равномерного усиления воздействия (и, соответственно, увеличения Y) значения большинства характеристик макрозообентоса закономерно уменьшаются.
Интенсивность их уменьшения зависит от упругой устойчивости сообществ к воздействию.
Пока исходный видовой состав сообщества и определяемая им упругая устойчивость к воздействию сохраняются, значения количественных характеристик макрозообентоса уменьшаются несущественно (обычно – не более, чем на 15% от своих фоновых значений).
Потеря упругой устойчивости сообщества к воздействию обычно проявляется в исчезновении из биотопа особей не какого-либо одного, а сразу многих стенобионтных видов. Их совместное исчезновение вызывает скачкообразное уменьшение большинства количественных показателей сообщества (на 30 – 60 % от фоновых значений, обычно – на 40-50%). Резкое изменение видового состава и количественных структурно-функциональных характеристик, происходящие при потере упругой устойчивости макрозообентоценоза, определяются как его первая катастрофа.
У большинства биоиндикационно значимых количественных характеристик макрозообентоса изоболы, очевидно, могут считаться подобными друг другу и границе ОСУ в системе координат, сопоставленных нормированным по уравнению (27) значениям комбинируемых факторов. Поэтому зависимость значений этих характеристик от изоболического показателя многофакторного воздействия Y обычно выражена достаточно чётко и хорошо аппроксимируется соответствующими функциями благополучия макрозообентоценоза.
Основной функцией благополучия макрозообентоценоза от многофакторного воздействия является его упругая устойчивость к данному воздействию (упругость). По определению, эта функция благополучия дискретна (точка разрыва соответствует значению аргумента Y=1) и может принимать лишь два различных значения. При уровне воздействия Y < 1 упругость сохраняется (значение данной функции благополучия равно единице), при Y > 1 упругость утрачивается (значение функции равно нулю).
Остальные функции благополучия макрозообентоценоза выражают зависимость его количественных биоиндикационно значимых характеристик (разд. 4.2, 4.3) от уровня многофакторного воздействия Y. Практика показывает, что графики функций благополучия макрозообентоценозов от уровня многофакторного воздействия довольно разнообразны, однако могут быть типизированы.
В зависимости от особенностей реакции характеристик сообщества, уже утратившего упругость, на дальнейшее возрастание воздействия (Y>1), могут быть естественно выделены следующие три основные типа функций благополучия сообществ от изоболического показателя (рис. 36).
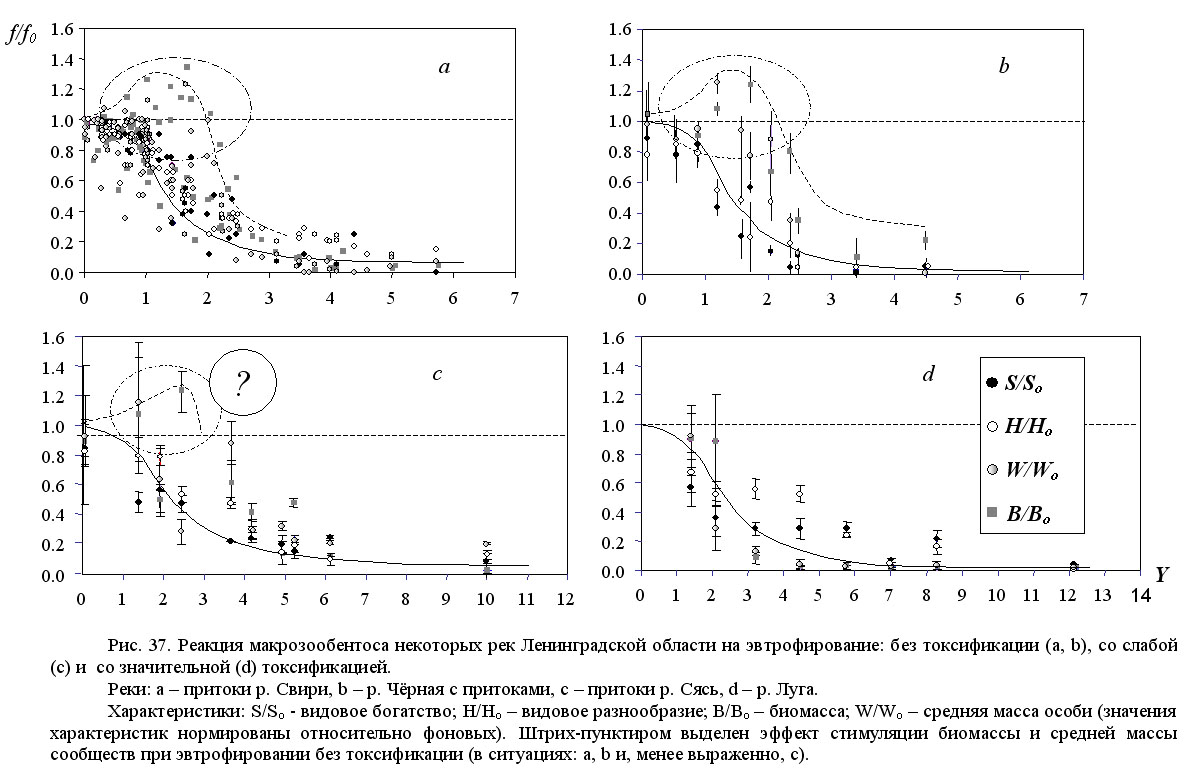
Тип I. После первой катастрофы дальнейшее усиление воздействия вызывает плавное, постепенное уменьшение значений функций благополучия, асимптотически стремящихся к нулю или иному минимальному значению (без второй катастрофы). График такой функции благополучия сообщества представляет собой монотонную нисходящую S-образную кривую (рис. 36, кривая I; практический пример – на рис. 37d).
Тип II. После первой катастрофы дальнейшее усиление воздействия до определённого уровня не вызывает существенных изменений значений функции. Однако при некотором, критическом уровне воздействия повторно происходит резкое обеднение видового состава сообщества и связанное с этим скачкообразное уменьшение значений функции благополучия: происходит вторая катастрофа макрозообентоценоза. Вторая катастрофа некоторых донных сообществ наблюдалась нами при уровне воздействия, примерно втрое превосходящем уровень потери их упругости и первой катастрофы (Y » 3). График такой функции благополучия сообщества представляет собой монотонную нисходящую двухступенчатую кривую (рис. 36, кривая II).
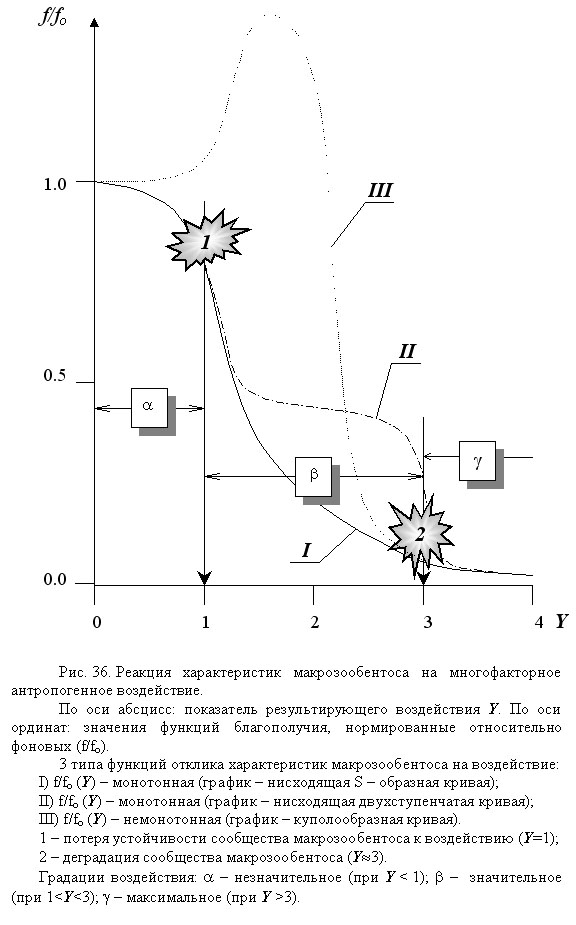
Сравнение примеров, приведённых на рисунках 29, 33 и 35, позволяет убедиться, что степень выраженности второй катастрофы в разных ситуациях может существенно варьировать. Остаётся неясным, является ли вторая катастрофа в градиенте воздействия менее обязательной, характерной и отчётливой, чем первая, или же это обусловливается лишь организационными трудностями её изучения. Как показано выше (разд. 5.1.2, 5.2.3), по целому ряду объективных причин ситуацию второй катастрофы в натурных условиях обнаружить намного сложнее, чем первой.
Тип III. Усиление воздействия сначала до некоторого уровня вызывает увеличение значений функции благополучия, а затем, превысив этот уровень, наоборот, определяет их резкое уменьшение. Иногда так реагируют на эвтрофирование (не связанное с токсификацией) количественные характеристики обилия макрозообентоса (биомасса, плотность, скорость образования продукции). Так, например, в заиленных биотопах р. Паши и её притоков умеренное эвтрофирование стимулирует увеличение указанных характеристик донных сообществ за счёт экспансии эврибионтных бентонтов (комментарий к рис. 8 в разд. 2.3.3; пример № 9). В этом случае график функции благополучия представляет собой немонотонную куполообразную кривую (рис. 36, кривая III; практические примеры – на рис. 37a, 37b).
В зависимости от свойств биотопа и от характера оказываемого воздействия, этот стимулирующий эффект может быть выражен в самой различной степени. Например, в той же р. Паше и её притоках он совершенно отсутствовал в биотопах с твёрдыми, слабо заиленными грунтами (комментарий к рис. 8 в разд. 2.3.3; пример № 9). При техногенном эвтрофировании водного объекта, отягощённом токсификацией, описанный стимулирующий эффект может проявляться слабо, нечётко (как, например, при воздействии ОАО "Бокситогорский глинозём" на притоки р. Сяси: рис. 37с) или же, вообще, отсутствовать (как при воздействии ООО "ПГ Фосфорит" на р. Лугу: рис. 37d).
Таким образом, между выделенными основными тремя типами функций благополучия макрозообентоценоза от уровня многофакторного воздействия нет сколько-нибудь чётких границ и возможны любые промежуточные варианты.
В связи с этим целесообразно считать основным, наиболее универсальным именно первый, простейший тип реакции макрозообентоценозов на многофакторные воздействия. По-видимому, этот тип функции благополучия сообщества от изоболического показателя Y должен быть положен и в основу нормирования многофакторных воздействий на водные объекты по состоянию биоиндикатора–макрозообентоса. Если предельно допустимый уровень многофакторного антропогенного воздействия устанавливается, исходя из предельно допустимого уменьшения значений функций благополучия первого типа, то при этом заведомо предотвращаются и недопустимые изменения значений функций второго и третьего типов (рис. 36).
Следовательно, экологические нормативы допустимых изменений макрозообентоса (как индикатора состояния гидроэкосистемы) целесообразно разрабатывать на основании функций его благополучия от изоболического показателя многофакторных воздействий Y первого типа.
Такая функция благополучия может быть хорошо аппроксимирована логистическим уравнением:
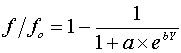 ,
, (51)
(51)
где f/fо – характеристика макрозообентоса, значение которой в изучаемых импактных условиях нормировано относительно синхронного ей фонового значения; a = const = 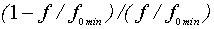 ; b= const; f/fо min= const – нижний предел значений функции (при Y ® +Ґ ).
; b= const; f/fо min= const – нижний предел значений функции (при Y ® +Ґ ).
Сравнительный анализ частных значений параметров уравнения (51), описывающих реакцию различных характеристик макрозообентоценозов на разнообразные многофакторные воздействия, показывает, что вариабельность этих значений и достоверность их различия обычно невелики (некоторые примеры приведены в табл. 14). Это позволило вывести единое уравнение зависимости нормированных характеристик макрозообентоценозов от изоболического показателя многофакторных антропогенных воздействий Y с параметрами: a = 22.8± 2.4, b= –1.53± 0.13.
Поскольку при указанных значениях параметров доля общей дисперсии значений большинства характеристик макрозообентоса, объясняемая уравнением (51), обычно превышает 90-95%, достигаемая при этом точность аппроксимации может быть признана удовлетворительной, а уравнение – пригодным для использования в целях экологического нормирования многофакторных воздействий на гидроэкосистемы.
Таблица 14.
Примеры частных значений параметров уравнения (51) для некоторых гидроэкосистем (выборочно для функций благополучия первого типа)
|
Гидроэкосистемы: |
Параметры |
|||||
|
f/fо |
a |
b |
ma/a |
mb/b |
r |
|
|
Водоём-охладитель Рязанской ГРЭС |
S/Sо |
51.7 |
-1.58 |
10.2 |
2.2 |
-0.74 |
|
Kso |
39.9 |
-1.67 |
10.1 |
2.0 |
-0.74 |
|
|
H/Hо |
36.6 |
-1.36 |
11.4 |
2.0 |
-0.68 |
|
|
B/Bо |
51.7 |
-1.58 |
10.2 |
2.2 |
-0.75 |
|
|
W/Wо |
15.7 |
-1.15 |
12.3 |
4.1 |
-0.64 |
|
|
р. Паша и её притоки |
S/Sо |
38.3 |
-1.60 |
8.1 |
1.7 |
-0.92 |
|
Kso |
27.1 |
-1.79 |
6.6 |
1.2 |
-0.91 |
|
|
H/Hо |
20.3 |
-1.23 |
10.3 |
3.2 |
||
|
B/Bо |
34.9 |
-1.84 |
8.3 |
1.4 |
-0.88 |
|
|
W/Wо |
19.0 |
-1.65 |
9.2 |
1.8 |
-0.80 |
|
|
р. Луга |
S/Sо |
18.7 |
-1.31 |
8.3 |
8.4 |
-0.90 |
|
Kso |
22.3 |
-0.88 |
7.4 |
14.1 |
-0.94 |
|
|
H/Hо |
19.2 |
-0.97 |
9.0 |
12.2 |
-0.83 |
|
|
B/Bо |
19.8 |
-1.35 |
11.1 |
15.3 |
-0.89 |
|
|
W/Wо |
28.7 |
-1.54 |
7.8 |
9.7 |
-0.95 |
|
Примечание: a, b – параметры уравнения (51); ma/a, mb/b – относительные ошибки их средних значений, %; r – коэффициент корреляции; S/Sо, H/Hо, Kso, B/Bо и W/Wо – нормированные значения видового богатства, разнообразия, сходства с фоновым видовым составом, биомассы и средней массы особи в сообществе, соответственно.
При уровне многофакторного антропогенного воздействия, приблизительно трёхкратно превышающем уровень потери устойчивости (Y>3), макрозообентоценоз, независимо от типа его предыдущей реакции, приходит к практически полной деградации (рис. 36). В его составе остаётся лишь несколько наиболее эврибионтных видов, особи которых немногочисленны или встречаются спорадически. Значения большинства функций благополучия при Y>3 не превышают 20% от фоновых, вне зависимости от типа реакции соответствующих характеристик сообщества на данное воздействие. Это позволяет предложить следующую единую классификацию уровней многофакторного антропогенного воздействия на гидроэкосистемы, основанную на характерной реакции наиболее универсального биоиндикатора – макрозообентоса (рис. 36).
1) a -диапазон значений Y ("незначительное" воздействие): упругая устойчивость сообществ к воздействию сохраняется, значения всех их количественных характеристик отклоняются от фоновых не более, чем на 15 % (f/fo і 0.85);
2) b -диапазон значений Y ("значительное" воздействие): упругая устойчивость сообществ к воздействию утрачена, произошла их первая катастрофа;
3) g -диапазон значений Y ("максимальное" воздействие): упругая устойчивость сообществ к воздействию утрачена, произошла их деградация, значения всех их количественных характеристик не превышают 20 % фоновых (f/fo Ј 0.20).
Данная классификация может быть положена в основу оценки и нормирования комбинированных (многофакторных) антропогенных воздействий на разнотипные водные объекты.
наверх
"Монография об изоболическом методе"
на главную страницу